This way a complex number is defined as a polynomial with real coefficients in the single indeterminate i for which the relation i 2 1 0 is imposed. The absolute value of a complex number is defined by the Euclidean distance of its corresponding point in the complex plane.

Absolute Value Of Complex Numbers A Plus Topper
Complex Numbers
How To Find The Absolute Value Of A Complex Number
A if a is greater than or equal to zero.
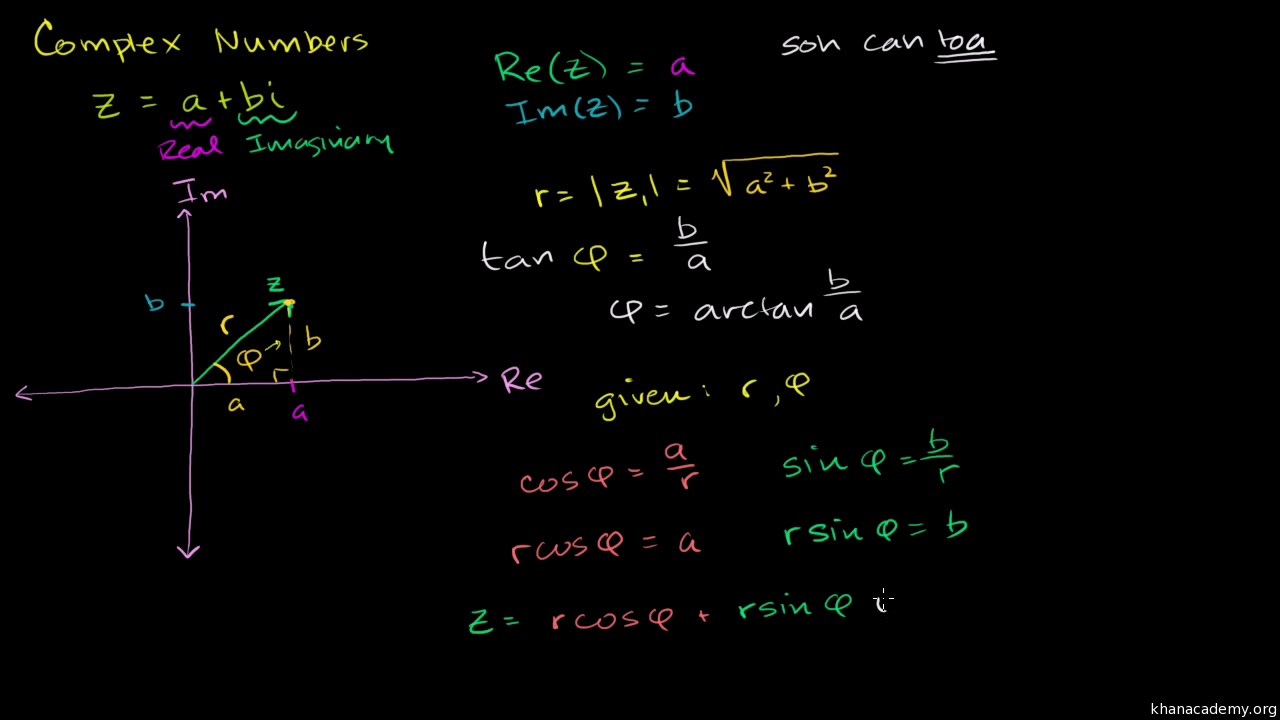
Absolute of complex number. Complex numbers is vital in high school math. Why is the absolute value of a complex number the same as its magnitude. The complex conjugate of a complex number is the number with the same real part and the imaginary part equal in magnitude but are opposite in terms of their signs.
For example 3 3 but 4 4. This can be summarized as follows. And is in the second quadrant since that is the location the complex number in the complex plane.
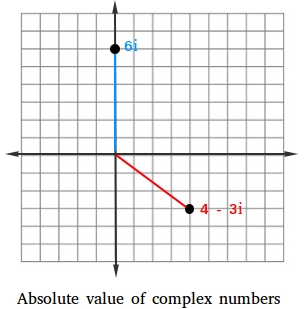
Since 5 is at 5 units distance from the origin 0 the absolute value of 5 is 5 55. Let z x iy where x and y are real and i -1. We can get the absolute value of an integer complex number or a floating number using the abs function.
The exponential form of a complex number is. The absolute value of complex number is also a measure of its distance from zero. Absolute Value of a Complex Number The absolute value of a complex number a b i also called the modulus is defined as the distance between the origin 0 0 and the point a b in the complex plane.
Since the complex numbers are not ordered the definition given at the top for the real absolute value cannot be directly applied to complex numbersHowever the geometric interpretation of the absolute value of a real number as its distance from 0 can be generalised. Perform operations like addition subtraction and multiplication on complex numbers write the complex numbers in standard form identify the real and imaginary parts find the conjugate graph complex numbers rationalize the denominator find the absolute value modulus and argument in this collection of printable complex number worksheets. Finding the magnitude and phase of complex exponential signals.
Absolute value and angle. Express 5cos 135 j sin 135 in exponential form. The absolute value of a number measures its distance to the origin on the real number line.
So the absolute value of the complex number is the positive square root of the sum of the square of real part and the square of the imaginary part ie Proof. However instead of measuring this distance on the number line a complex numbers absolute value is measured on the complex number plane. Instead we will mostly use the geometric definition of the absolute value.
And jsqrt-1 Example 1. Recall that the absolute value x of a real number x is itself if its positive or zero but if x is negative then its absolute value x is its negation x that is the corresponding positive value. Absolute Value of A Real VS.
The calculator uses the Pythagorean theorem to. This formula is applicable only if x and y are positive. Complex number absolute value angle review.
A complex number is a number of the form a bi where a and b are real numbers and i is an indeterminate satisfying i 2 1For example 2 3i is a complex number. Graph the set of x such that 1 x 4 and x is an integer see Figure 2. For a real value a the absolute value is.
The absolute value of a number is easy to find and the theory behind it is important when solving absolute value equations. The forget the minus sign definition of the absolute value is useless for our purposes. R e j theta r is the absolute value of the complex number the same as we had before in the Polar Form.
The first one well look at is the complex conjugate or just the conjugateGiven the complex number z a bi the complex conjugate is denoted by overline z and is defined to be beginequationoverline z a - biendequation In other words we just switch the sign on the imaginary part of the number. Conjugate of a Complex Number. Review your knowledge of the complex number features.
But the following method is used to find the argument of any complex number. If youre using a calculator to find the value of this inverse tangent make sure that you understand that your calculator will only return values in the range - fracpi 2 theta fracpi 2 and so you may get the incorrect value. Problem with absolute value of addition of complex numbers.
The abs function always returns a positive number even when the input value is negative or a complex number. The absolute value or modulus is the distance of the image of a complex number from the origin in the plane. Usually we have two methods to find the argument of a complex number i Using the formula θ tan1 yx here x and y are real and imaginary part of the complex number respectively.
Using the pythagorean theorem Re² Im² Abs² we are able to find the hypotenuse of the right angled triangle. The absolute value function strips a real number of its sign. Then the non negative square root of x2 y2 is called the modulus or absolute value of z or x iy.
Definition of Modulus of a Complex Number. If the argument x integral value is a float or integer then the resultant absolute value will be an integer or float. The absolute value of a complex number also called the modulus is a distance between the origin zero and the image of a complex number in the complex plane.
Absolute value means distance from zero on a number line. An important concept for numbers either real or complex is that of absolute value. Based on this definition complex numbers can be added and multiplied.
If you think of a number line with zero in the center all youre really doing is asking how far away you are from 0 on the number line. In the case of a complex number r represents the absolute value or modulus and the angle θ is called the argument of the complex number. The polar form of a complex number z a b i is z r cos θ i sin.
When graphing inequalities involving only integers dots are used. Let us consider the mode of the complex number z is extended from 0 to z and the mod of a. - Adding subtracting multiplying dividing complex numbers - Complex plane - Absolute value angle of complex numbers - Polar coordinates of complex numbers Our mission is to provide a free world-class education to anyone anywhere.
X1 x 4 x is an integer Figure 2. The abs function in Python is used for obtaining the Python absolute value or the positive value of a number. Convert between them and the rectangular representation of a number.
The equation above is the modulus or absolute value of the complex number z. Google Classroom Facebook Twitter. The abs is a built-in method used to get the absolute value in which it converts a negative value into a positive value and if there is a positive value then it doesnt change.
θ is in radians. The absolute value or modulus of a real number is the corresponding nonnegative value that disregards the sign.
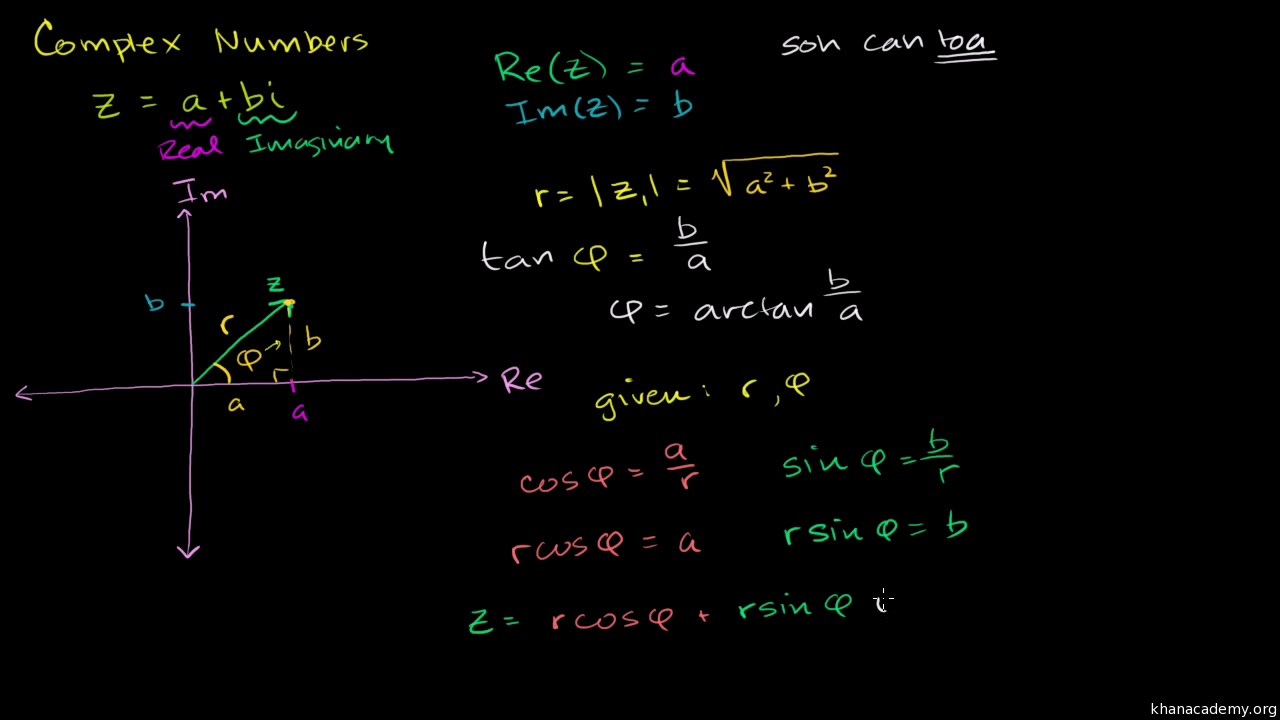
Absolute Value Angle Of Complex Numbers Video Khan Academy

Solved Plot The Complex Number And Find Its Absolute Value Chegg Com
Complex Numbers

How Do You Find The Absolute Value Of A Complex Number Virtual Nerd

Complex Numbers Imaginary Number By Solomon Xie All Math Before College Medium

5 6 Complex Numbers What Is A Complex Number A Complex Number Is Made Up Of Two Parts A Real Number And An Imaginary Number Imaginary Numbers Ppt Download
Absolute Value Of Complex Number
Addition And Subtraction Of Complex Numbers Examples Multiplication And Division Of Complex Numbers Examples Graphing Complex Numbers
